Introduction
Inferring individual treatment effects has great potential for personalised recommendations. That is, what would happen to an individual given the treatment in question, and how it changes across different treatments. For instance, consider a set of covariates X that describes an individual, a treatment status T and an outcome Y we observe for said individual after receiving the treatment. Assuming the participant did receive an actual treatment (T=1) and we observed an associated outcome Y(1|X), one can ask how the outcome would differ if said individual was in the control group (T=0), that is, Y(0|X) =? Also, what is the effect of the treatment on that specific individual, that is, Y(1|X) – Y(0|X) =?
This task is particularly challenging with observational data for multiple reasons, but which must be used in the absence of randomised experiments. One of the issues is nonrandom treatment selection that leads to very different covariate distributions among the treated and control units. For example, the data may include very few treated individuals past a certain age or of a specific occupation. This issue is more formally known as covariate shift where the learning target P(Y|X) remains unchanged, but the marginal distributions of the covariates P(X) differ between treated and control units.
One common solution to this problem is sample reweighing, often based on propensity scores. This approach generally performs well for estimating treatment effects averaged across the common support of X, but the model’s parameters are often misspecified at pointsoutside the observed support, resulting in inaccurate treatment estimates at said individual data points. In other words, reweighing methods perform well in average treatment effect (ATE) estimation tasks, but struggle with conditional average treatment effect (CATE) ones due to model misspecification.
Model Misspecification and Biased Estimators
Figure 1 demonstrates how a biased dataset can lead to misspecified models that in turn result in biased estimators (Biased T and Biased C) that provide inaccurate CATE estimates. For an accurate CATE prediction, a much closer data fit is needed that involves less smooth modelling of data points, or undersmoothing. Such undersmoothed and unbiased models are represented by Unbiased T and Unbiased C curves in Figure 1.
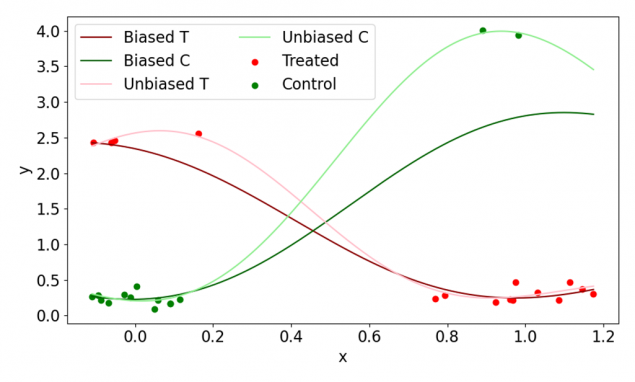
Figure 1. A synthetic example involving a single input feature X, outcome Y and binary treatment T. Note two heterogeneous groups (x < 0.5 and x > 0.5). T and C denote treated and control groups respectively.
Debiasing Generative Trees
The objective of this work is to obtain unbiased and undersmoothed causal estimators by undersmoothing the data itself as a data preprocessing step. Specifically, we incorporate recently proposed Generative Trees (Correia et al., 2020) to augment the data such that the causal estimators trained on them are more robust when it comes to CATE estimation.
In this approach, we use trees to identify heterogeneous subpopulations within data, distributions of which are modelled with Gaussian Mixture Models (GMMs). We then sample equally from said individual GMMs to reduce data imbalances and biases. A summary of the proposed framework, which we call Debiasing Generative Trees (DeGeTs), is depicted in Figure 2. In addition, by using a Random Forest instead of just a single Decision Tree, the framework can be generalised to a Debiasing Generative Forest (DeGeF).
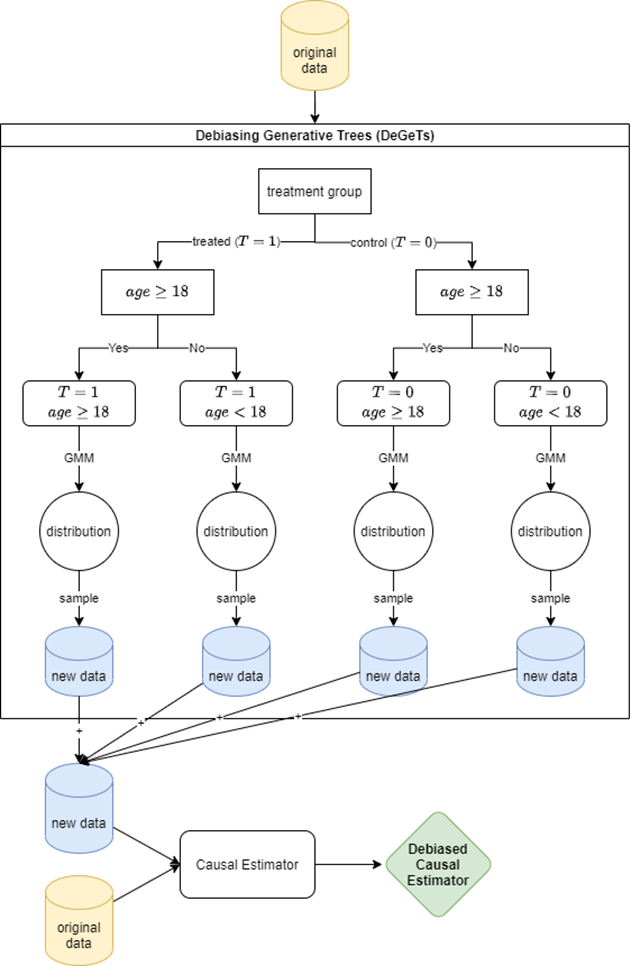
Figure 2. A diagram depicting the major building blocks and steps involved in the proposed Debiasing Generative Trees (DeGeTs) data augmentation method. First, a standard Decision Tree is built based on provided data. The distributions of the data points in the tree leaves are modelled with Gaussian Mixture Models (GMMs). We then sample new data points from modelled distributions that together form a new subset of data. Both original and new data are merged into a single dataset that is now debiased owing to the new data points that fill the gaps that previously caused biased estimates. Thus, a causal estimator trained on such data is now a Debiased Causal Estimator.
Results and Main Findings
To test the effectiveness of our method, we evaluated it on four well-established benchmark datasets and compared obtained performances to standard causal inference methods. All code and data are available online at https://github.com/misoc-mml/undersmoothing-data-augmentation.
Our main findings are as follows:
- The choice of model class can significantly affect the estimation performance.
- Standard reweighing methods can struggle with individualised effect estimation.
- Our proposed data augmentation approach is competitive with reweighing methods on ATEs and performs significantly better on CATEs.
- Our method achieves the desired undersmoothing effect through increased data complexity of the augmented data (see Figure 3).
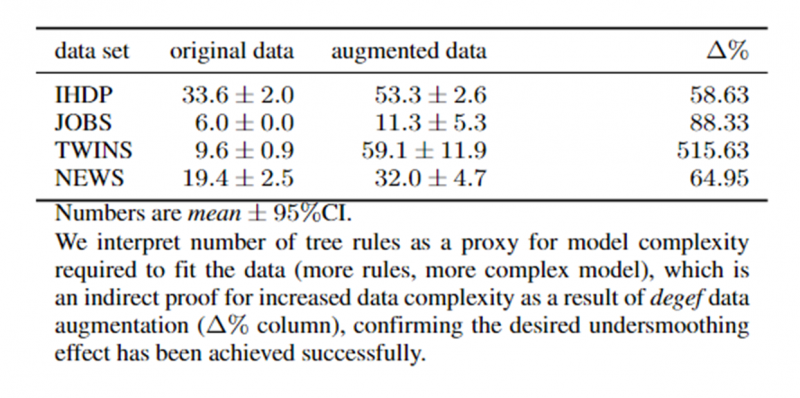
Figure 3. Number of rules in a pruned Decision Tree inferred from data across all four datasets. The proposed DeGeF data augmentation increases the number of inferred rules, which we interpret as an indirect sign of increased data complexity and indirect evidence for achieved undersmoothing.
The full results are available in our working paper (Machlanski et al., 2022) here.
References
Correia, A., Peharz, R., & de Campos, C. P. (2020). Joints in Random Forests. Advances in Neural Information Processing Systems, 33, 11404–11415.
Machlanski, D., Samothrakis, S., & Clarke, P. (2022). Undersmoothing Causal Estimators with Generative Trees (arXiv:2203.08570). arXiv. https://doi.org/10.48550/arXiv.2203.08570
