Introduction
Understanding how dataset covariates are causally linked to each other is very useful in data analysis as it reveals how the data were potentially generated in the first place. The task of inferring such causal relationships is often called causal discovery or (causal) structure learning due to the fact that the result is a graph with covariates as graph nodes and said relationships as edges between the nodes. Such causal graphs are a graphical representation of the data generation process (DGP) behind given data.
The algorithms that infer causal graphs from observational data are built upon machine learning (ML) methods. Furthermore, as evident from the literature and our previous work (Machlanski et al., 2023a), ML approaches heavily rely on hyperparameters (e.g. L1 sparsity penalty) to the extent that the correctness of specified hyperparameter values can make the difference between poor and state-of-the-art (SotA) prediction performance.
However, selecting correct hyperparameter values (a.k.a. tuning) is extremely challenging in structure learning due to the unsupervised nature of the task. That is, the true causal graph corresponding to the data at hand is unknown to the analyst. While the learning algorithms have been evaluated extensively in the literature, understanding how hyperparameter selection can affect algorithm choice and individual algorithms is clearly missing. This motivates the core questions of our work:
- Are hyperparameters as important in structure learning as in other areas?
- Do different algorithms perform similarly given access to a hyperparameter oracle?
- How robust are they against misspecified hyperparameters?
A Case of Two Variables
We start our analysis with a simple example that entails only two covariates X and Y. Our objective is to determine the existence and direction of the causal link between X and Y. There are three possible answers in this case: X causes Y (X → Y), Y causes X (X ← Y), or X and Y are not causally related to each other. One possible algorithm to solve this task involves fitting two regressors y = f(x) and x = g(y), measuring their prediction errors (ef and eg respectively), and deciding the direction of the causal link based on the lower prediction error (X → Y if ef < eg, X ← Y if ef > eg, and ‘no link’ otherwise). Then, as demonstrated by Figure 1, by only changing the number of allowed regression parameters, which is a hyperparameter in this case, we can end up with a different solution. This precisely constitutes the problem as the correct number of parameters is unknown a priori. By blindly trying different hyperparameter values, we can get opposing hypotheses (e.g. 2 and 8 parameters).
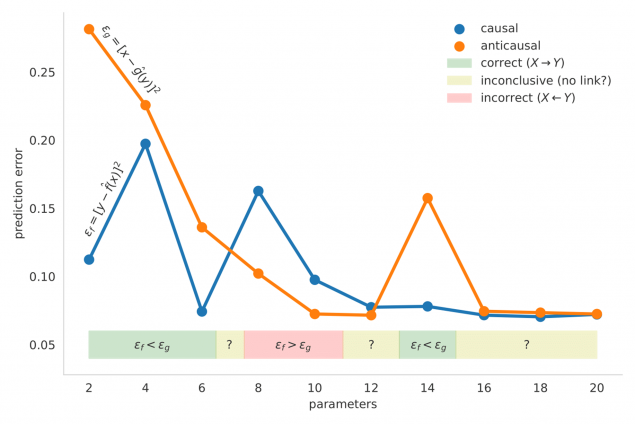
Figure 1. The number of regression parameters (X axis), a hyperparameter, clearly impacts prediction error (Y axis) and as a result predicted causal direction.
Further Experiments
Our simple analysis so far confirmed that hyperparameters and their selection do impact structure learning algorithms, at least in trivial cases. This motivates a more rigorous investigation of the issue and our experimental setup summarised in Figure 2. More precisely, we explore some seminal structure learning algorithms and their performances under different hyperparameter selection scenarios, tested on datasets of varying levels of difficulty. The code is available online at https://github.com/misoc-mml/hyperparams-causal-discovery.
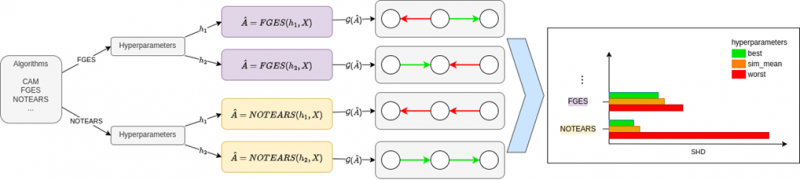
Figure 2. Summary of key ideas behind the study. We explore different algorithms, hyperparameters and their values, and how different choices affect the final performance of structure learning. Note how predicted structures vary between different hyperparameter values (green – correct edge; red – incorrect).
Results and Main Findings
- Algorithms differ significantly in performance even with access to hyperparameter oracle. The best choice still depends on the data (i.e. there are no free lunches).
- Algorithms vary in robustness to hyperparameter misspecification. This means some algorithms are safer to use than others. And as shown in Figure 3, strong performance under correct hyperparameters does not necessarily translate to robustness.
- To select the best algorithm for a given problem, one must consider not only DGP’s properties, but also the potential quality of selected hyperparameter values. In other words, assuming the best hyperparameters (left ends of the bars in Figure 3), a different algorithm will be preferrable depending on the dataset. But a different algorithm might be preferred in case of poorly chosen hyperparameter values (right ends of the bars).
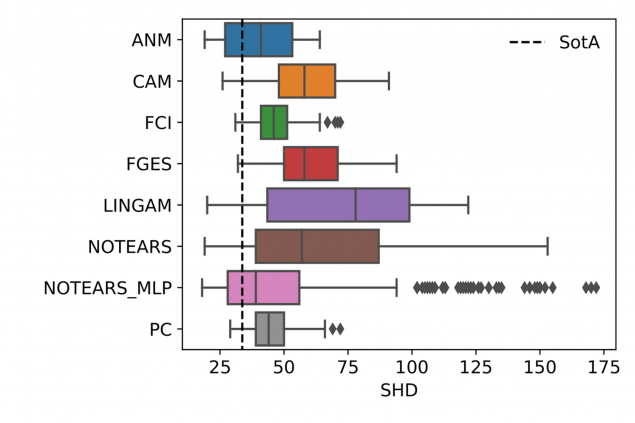
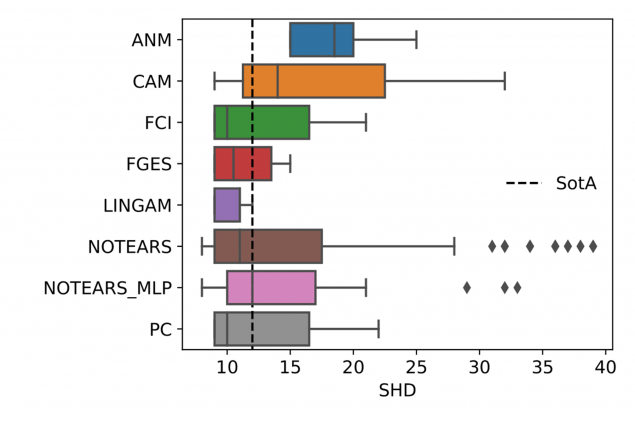
Figure 3. Algorithm performances across all explored hyperparameters and values. Left: SynTReN dataset, right: Sachs dataset. SHD is structural Hamming distance (lower is better). SHD of 0 means the predicted graph is the same as the true graph. Note that: a) many algorithms can surpass SotA with the right hyperparameters, and b) robustness to misspecified hyperparameters varies substantially between algorithms and datasets.
The full results are available in our working paper (Machlanski et al., 2023b) here.
References
Machlanski, D., Samothrakis, S., & Clarke, P. (2023a). Hyperparameter Tuning and Model Evaluation in Causal Effect Estimation (arXiv:2303.01412). arXiv. https://doi.org/10.48550/arXiv.2303.01412
Machlanski, D., Samothrakis, S., & Clarke, P. (2023b). Robustness of Algorithms for Causal Structure Learning to Hyperparameter Choice (arXiv:2310.18212). arXiv. https://doi.org/10.48550/arXiv.2310.18212
