Introduction
The estimation of causal effects from observational data is a fundamentally important problem in social research and indeed all scientific research. Consider an exposure D such as living in poor quality housing (accommodation affected by e.g. damp and mould) where D = 1 indicates people living in poor-quality housing and D=0 indicates they do not. Suppose we also measure outcome Y the health of every individual in our study at the end of a fixed observation period. The causal effect of poor quality housing D on health Y is the difference between two alternative scenarios, Y(1) – Y(0), where Y(1) is someone’s health had they lived in poor quality housing and Y(0) the health of the same person had they not, with everything else in the two scenarios held to be exactly the same. The average treatment effect (ATE), for example, is the average of these differences taken over everyone in the population.
The fundamental problem of causal inference is that causal effects cannot be directly estimated because the counterfactual quantities (Y(0) for those living in poor quality housing and Y(1) for those not living in poor quality housing) are not observed. Were an experiment carried out where people were randomized to live in poor quality housing, we could have estimated the ATE by taking the difference between mean health in the two groups. But in observational studies, where people end up non-randomly `selected’ into poor quality housing, the difference between the two groups confounds the actual effect of poor housing with pre-existing systematic differences between the sorts of people ends up in poor quality housing and those who do not. These differences must be adjusted for. Causal estimators (CE) have been devised to estimate causal parameters like ATE and conditional average treatment effects (CATE) which capture how causal effects vary between different groups of people (e.g. doubly robust estimation). Many of these make use of Machine Learning (ML) methods as sub-components or base learners (e.g. to model response propensities). ML learners are highly flexible, capable of handling high-dimensional non-linear functions, but their hyperparameters (e.g. L1 sparsity penalty or L2 regularisation strength) must be tuned to the dataset at hand to avoid large estimation errors.
In practice, finding the best hyperparameters tailored to a specific dataset requires Model Evaluation (ME) using performance-validation metrics. This task is especially difficult in causal effect estimation because the estimation target is the causal effect expressed as the difference Y(1) – Y(0), where Y(1) and Y(0) represent outcomes under and no treatment respectively for the same individual, meaning one of the outcomes is always missing. ME metrics, however, are often based on goodness-of-fit measures that involve only observed data (Y=Y(1) for treated, Y=Y(0) for not treated), hence called observable metrics. Ideally, we would measure prediction error directly on Y(1) – Y(0), but the corresponding potential metric is inaccessible (see Figure 1 for a graphical demonstration of the problem). This issue created the need to develop more advanced model evaluation procedures suited specifically to causal estimation settings.
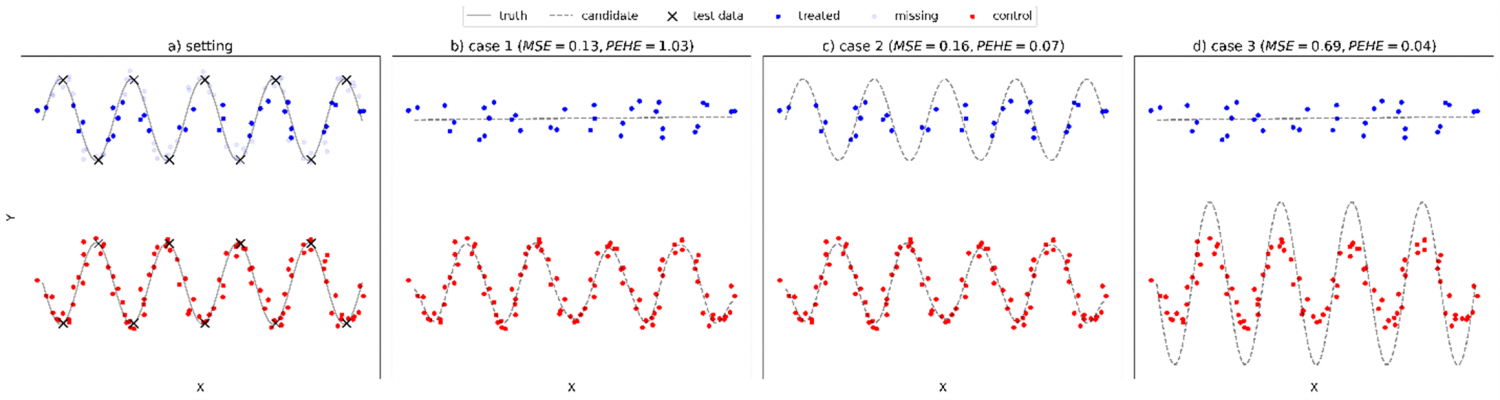
Figure 1. A toy example demonstrating the difference between observable (MSE) and potential (PEHE) model evaluation metrics and their varying response to modelling choices.
This Work
The developments resulted in practitioners having to make modelling decisions in four different areas: CEs, ML base learners, hyperparameters and ME metrics. Motivated by inconsistent recommendations, our recent study investigates the complex relationship between the four aspects (Machlanski et al., 2023). More precisely, we set out to better understand the following.
- How hyperparameters of ML base learners affect causal effect estimation performance?
- How model evaluation metrics affect the quality of hyperparameter tuning?
- How hyperparameter tuning and model evaluation vary across causal estimators and ML base learners?
Our comprehensive experimental setup focuses on methods used commonly by practitioners. It involves all combinations of 7 CEs and 9 ML base learners. We also include 6 ME metric families with multiple variations that involve both general ML metrics as well as the ones built specifically for causal settings. Each ML learner has a set of possible hyperparameters and values, all of which are explored exhaustively. We follow good modelling practices by incorporating cross-validation and cross-fitting where applicable to avoid overfitting. All experiments are run against four well-established causal inference benchmark datasets, namely IHDP, Jobs, Twins and News. We explore the combinations of CEs, ML learners, hyperparameters and ME metrics as exhaustively as possible in order to study the problem thoroughly. The accompanying code and datasets are publicly available online at https://github.com/misoc-mml/hyperparam-sensitivity.
Results and Main Findings
- Finding optimal hyperparameters of ML learners is enough to reach state-of-the-art performance in effect estimation, regardless of selected causal estimators and base learners. Thus, finding and selecting good hyperparameters is much more important and influential for causal estimation than deciding which causal estimator or ML base learner to use.
- Given how important hyperparameters are, using default hyperparameters or performing very little tuning is considered risky as such practice delivers sub-optimal estimation performances. This is demonstrated in Figure 2, where estimators with optimal hyperparameters consistently and significantly outperform those with default hyperparameters.
- In practice, hyperparameter search is data-driven, heavily relying on model evaluation techniques and their accuracy of identifying optimal hyperparameters. As such, model evaluation metrics are as critically important as hyperparameter tuning. However, our results suggest that commonly used (observable) evaluation metrics tend to select sub-optimal hyperparameters, significantly reducing causal estimation performance that would be otherwise possible (with potential metrics). Further research into causal model evaluation, not new estimators, is needed for meaningful progress.
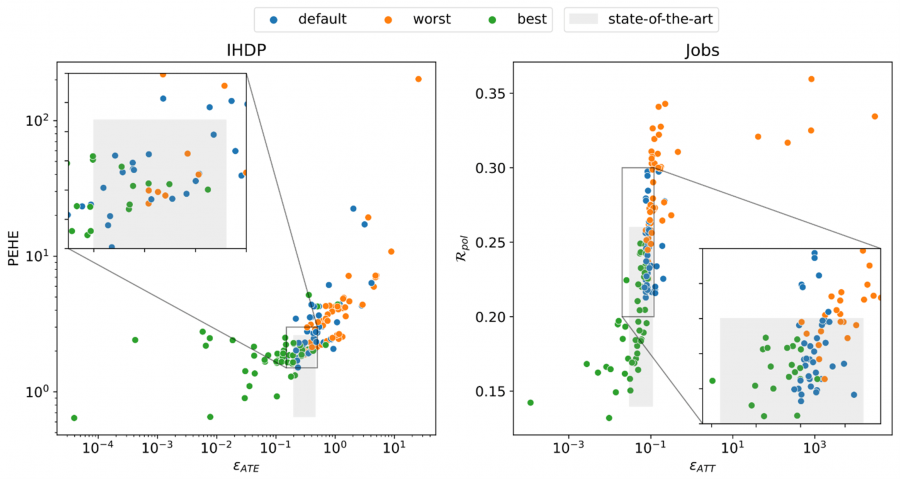
Figure 2. Performances of causal estimators on IHDP and Jobs datasets. Each data point represents a different estimator. Colours denote the quality of selected hyperparameter values. Lower is better for all metrics.
The full results are available in our working paper (Machlanski et al., 2023) here.
References
Machlanski, D., Samothrakis, S., & Clarke, P. (2023). Hyperparameter Tuning and Model Evaluation in Causal Effect Estimation (arXiv:2303.01412). arXiv. https://doi.org/10.48550/arXiv.2303.01412
